eScience Lectures Notes : Mathematics for Computer Graphics
Slide 1 : 1 / 23 : Mathematics for Computer Graphics
Ref : Computer Graphics / Foley - VanDam - Feiner - Hughes
This part is somewhat theoritical, but it should not be
too difficult with a simple mathematical background
Slide 2 : 2 / 23 : Why Mathematics ?
Why Mathematics ?
-
To have fun
-
To get about 1/3 of the point at the final exam
-
To understand the theory of Computer Graphics
-
To place your 3D objects and your viewpoint in the right position !
-
To understand Raytracing, Physical modelling of ball animation, Surface
modelling, or other 3D or 2D issues
-
Slide 3 : 3 / 23 : Vector Space
Vector Space
Set of elements called vectors, with 2 operations with certain properties:
Usually we will note a vector in boldfaced letters or
with an arrow above it
1 ) Addition of vectors : commutative, associative, with an identity element
and each element must have inverses
- u + v = v + u
- u + ( v + w ) = (u + v
) + w
- there is 0 such as for any vector v, 0 + v =
v
- for every vector v, there is another vector w such as v
+ w = 0 . w is written " -v "
2 ) Scalar Multiplication : associative and distributive
- (ab)v = a (bv)
- 1v = v
- (a + b)v = av + bv
- a(v + w) =av + aw
Given those two operations, we may define a "linear combination"
of a set of vector v1, ... vn : any vector of the form
a1v1 + a2v2 + ... anvn
Example of Vector Space : Rn (the set of all ordered n-tuples of real number)
is a vector space
Sub example : R3 :
/ r1 / 1 / 4 / 5
| r2 ...... ex : | 3 + | 5 = |12
\ r3 \ 6 \ 2 \ 8
Slide 4 : 4 / 23 : Plane Vector Splace
One particular Vector Space : The Plane
We chose an origin, and every point of the plane is matched with the vector
that links the point to the chosen origin
We may then easily define ...
The addition of two vector (the parallelogram rule)
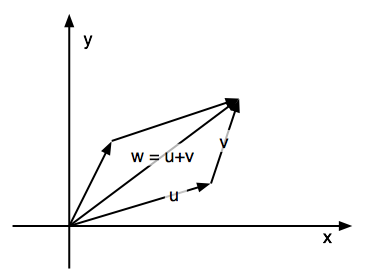
|
The multiplication of a vector by a scalar
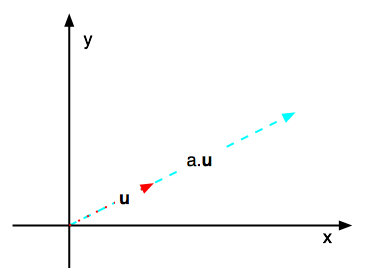
|
The vector 0 : the one which is matched with the chosen origin
Slide 5 : 5 / 23 : Affine Space
Affine Space
A set in which geometric operations make sense, but in which there is no distinguished
point
(i.e. no origin such as in a vector space)
A affine space consists of a set, called the points of the affine space, an
associated vector space and two operations which connect the affine and the
vector space
Given 2 Point P and Q, we can form the difference of P and Q which lies in
the vector Space
P - Q = v
Given a point P and a vector u, we can add u to P and get another point in
the affine space
P = Q + v
Properties to satisfy
(P + v) + u = P + (v + u)
P + u = P if and only if u = 0
Affine combination of the points P and Q by the real number t : a point such
as :
P + t (Q-P) ....... if a + b = 1 ... new notation : aP + bQ <=>
P + b (Q-P)
NB : convex combination <=> 0 <= t <= 1
if t1 + t2 + ... tn = 1
t1 P1 + t2 P2 + ... tn Pn <=> P1
+ t2 (P2 - P1) + ... tn (Pn - P1)
NB : convex affine combination <=>
0 <= ti <= 1
Slide 6 : 6 / 23 : Various other curiosities
Various other curiosities
Equation of a Line in an Affine Space defined by two point P and Q and t a
real
set of point of the form (1-t) P + t Q
Equation of a Plane in an Affine Space defined by three not collinear point
P, Q and R
set of point of the form (1-s) ((1-t) P + t Q) +s R
Vector and affine linear subspace are resp. vector and affine space
V : Non empty subset which is stable through the addition and the multiplication
by a real
A : such as the set of the difference between any element of A is a linear
vector subspace
Example
Vector subspace of R4
/ x
| y
| z
\ 0
Affine Subspace of R4 : standard affine 3 space
/ x / x1 - x2
| y v1 - v2 = | y1 - y2 belongs to the previous
| z | z1 - z2 vector subspace of R4
\ 1 \ 0
Slide 7 : 7 / 23 : Cartesian coordinate system
The cartesian plane : set of point labeled with coordinate (x, y) is an affine
space
Two usual cartesian reference frames
"Maths" frame
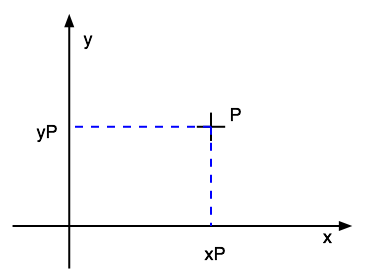
|
"Computer Graphics" frame
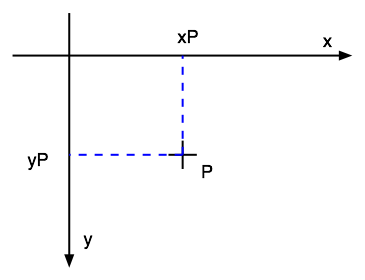
|
PS. : "Cartesian" comes from René
Descartes
Slide 8 : 8 / 23 : Cartesian coordinate system 3D
Cartesian coordinate system 3D
The Cartesian space : set of point labelled with coordinate (x, y, z) is an
affine space
Two different orientations
3 fingers or thumb or corkscrew rules
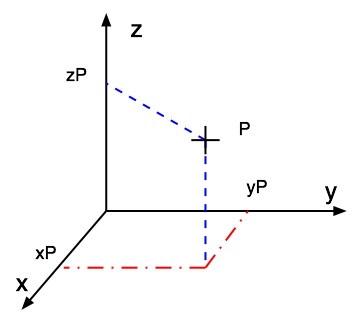
Right-handed system
Usual in Maths, Physics...
|
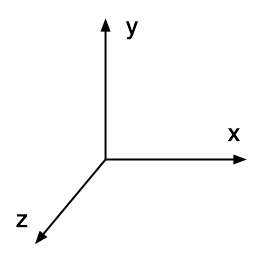 Java system
Java system
|
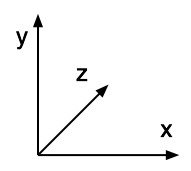 Left handed system
Left handed system
|
/ a1 / a2 / a2-a1
M | b1 P | b2 u = MP = | b2-b1
\ c1 \ c2 \ c2-c1
Slide 9 : 9 / 23 : Dot Product and Distance
Dot Product and Distance (2D, 3D, ...)
a.k.a. Scalar Product
/ x1 / x2
u.v = | y1 . | y2 = x1.x2 + y1.y2 + z1.z2
\ z1 \ z2
Distance between M and P :
u = MP
Dist (M,P) = ||u|| = SquareRoot(u.u) = SquareRoot( (a2-a1)2
+ (b2-b1)2 + (c2-c1)2 )
v = 0 <=> ||v|| = 0 <=> v.v
= 0
/ a1 / a2 / a2-a1
M | b1 P | b2 u = MP = | b2-b1
\ c1 \ c2 \ c2-c1
Slide 10 : 10 / 23 : Dot Product and Angle
Dot Product and Angle
u.v = ||u||.||v||.cos(uˆv)
if u and v are long enough ... (uˆv)
= acos(u.v / (||u||.||v||)
Trigonometric circle
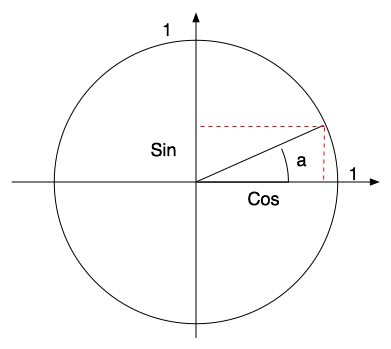
|
sin(0) = 0
sin(PI/2 rad) = 1
cos(0) = 1
sin(a) = opp/hyp
cos(a) = adj/hyp (Trigo + Thales)
if you know the cosine, you don't know the sign of the angle !
u.v = 0 <=> (u,v) orthogonal, perpendicular (Maths)
u.v <= epsilon <=> (u,v) orthogonal, perpendicular (Computing)
(or u = 0, or v = 0 ...)
|
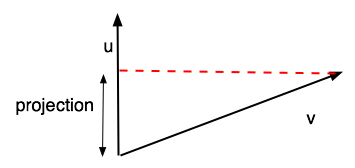
Length of the perpendicular projection of v on u ??
Length = u.v / || u || = (u/||u||).v
|
 |
Slide 11 : 11 / 23 : Cross Product
Cross Product
a.k.a. the vector product
/ x1 / x2 / y1.z2 - y2.z1
u x v = u ^ v = | y1 x | y2 = | x2.z1 - x1.z2
\ z1 \ z2 \ x1.y2 - x2.y1
u x v is a vector perpendicular to both u and v , which direction is given
by the usual right
handed rule, and the length, by :
|| u x v || = || u || . || v || . sin (uˆv)
now we are able to get the angle ...
Before going further, let's check those properties (again
?)
u x v is normal to the plane defined by u and v (and a chosen point)
if ( i, j, k ) are the set of vectors that define your right handed three-dimensional
coordinate system, then k = i x j
/ 1 / 0 / 0.0 - 1.0 / 0
i x j = i ^ j = | 0 x | 1 = | 0.0 - 1.0 = | 0 = k
\ 0 \ 0 \ 1.1 - 0.0 \ 1
All the usual right handed rules could be applied, the
3 fingers, the thumb and the others, the screwdriver and the corkscrew for the
French ...
Other simple problem : How to compute the normal to a plane ?
Slide 12 : 12 / 23 : How to get an orthogonal Vector .... in 2D
How to get an orthogonal Vector .... in 2D
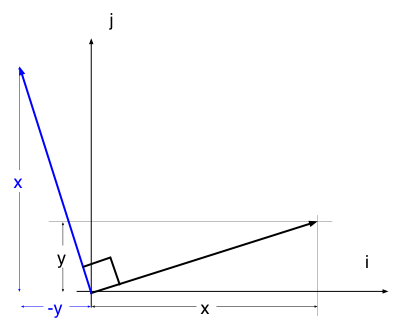
| x | -y | y
v = | y => w = | x or -w = | -x
Slide 13 : 13 / 23 : Orthogonal Vector .... in 3D
How to get an new cartesian coordinate system in 3D, starting from one vector.
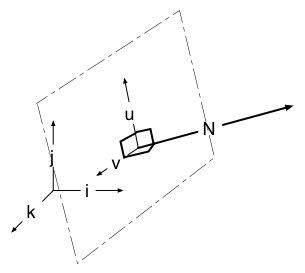
if N.j > Epsilon ( N et j not orthogonal ) => N
and k not parallel => k x N not null
Let's just define, arbitrarily, u
= k x N / || k x N ||
By construction, u is perpendicular to both k and N
then Let's define v = N x u / || N x u ||
With u and v, we've got an orthogonal basis (hamel basis) within
the plan normal to N
What if N and j are orthogonal ?
then N and j are not parallel => N x
j not null => u = N x j
What about continuity issues (would it
be better to use i : N x i ?)
An application : the envelope of a path
Slide 14 : 14 / 23 : Locus
Where could I Be ?
If I look at two landmarks (identifiable features with known coordinate) and
if I am able to measure the apparent angle between these two points, could I
derive my position from that observation ?
No, because there exist a full set of point (called a Locus of point) that
will accommodate these parameter.
Locus of point defined by a constant view angle from 2 fixed points.
Set of point defined by the fact that they form a given angle with two fixed
points (A et B, of the Euclidian Plane).
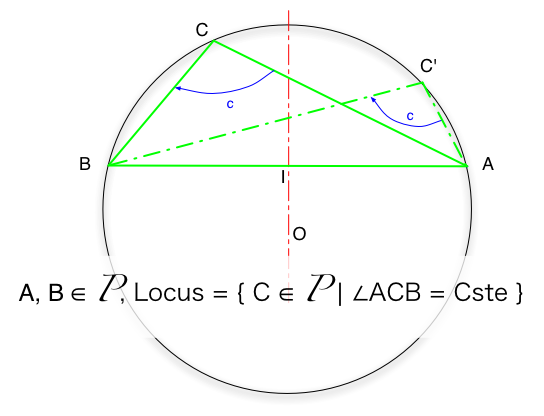
NB : Be careful to be coherent with the orientation of your
angles, and that the construction is not the same if the angle is acute (<90°)
or obtuse (>90°)
Slide 15 : 15 / 23 : Locus
Locus of point defined by a constant view angle from 2 fixed points
Set of point defined by the fact that they form a given angle with two fixed
points (A et B, of the Euclidian Plane).
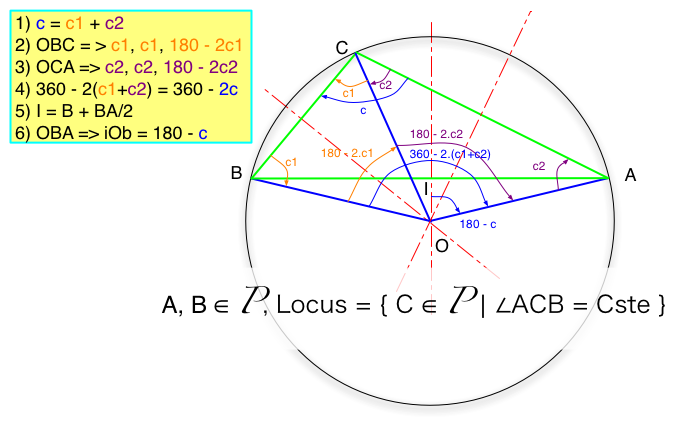
0) Given A, B and an angle c defined between
0 and 180°, positive from A to B. We will demonstrate that the set of point
C such as aCb = c is indeed the arc AB (which arc AB is defined by the relative
value of the angle compared to 90°). To achieve that, we consider one given
C point that verify aCb = c and we look at the centre of the circum(scribed
)circle for the triangle (ABC). We will indeed show that this circle can be
describe without referring to C, but just AB and the angle c, and that therefore
the possible set of C points are all on that circle.
1) Given ABC, it is well known that the circumscribed
circle has its circumcenter O at the intersection of the 3 perpendicular bisectors
of the triangle. Let's consider the two triangles (OCB) and (OAC) which share
the common edge [OC]. c = c1 + c2
2) In all triangles, the somme of the angles
equal to180. As O is on the perpendicular bisector of [CB], then (OCB) is a
isosceles and therefore oCb = cBo = c1. From those two fact the last angle bOc
= 180 - 2.c1
3) Likewise, in the isosceles triangle (OAC),
we get cOa = 180 - 2.c2
4) bOa = bOc + cOa = 180 - 2.c1 + 180 - 2.c2
= 360 - 2 c
5) I is the middle of [AB], and then on its
same perpendicular bisector as O. Therefore (IOB) is rectangle in I. Knowing
I, A and the angle iOa = bOa / 2 = 180 - c, it is possible to defined O, without
any reference to C. We have indeed demonstrate that given two fixed point A
and B and an oriented angle c, the set of point C such as aCb = c is on the
circle defined by its centre O and its radius OA.
NB. : Just note the effect of the orientation
of the angle and its value relative to 90° to the selection of the part
of the circle and the position of O relative to [AB]
links :
PS. Question : why is the intersection of
the 3 orthogonal bisectors the centre of the circumcircle ... ?
Slide 16 : 16 / 23 : Triangulation
Almost Triangulation : why you need at least two measures to guess where you
are ...
Triangulation : A method of fixing an unknown point (for example in navigation)
by making it a vertex of a triangle whose other vertices and angles are known
(Collins Dictionary of Mathematics).
Slide 17 : 17 / 23 : Triangulation with a compass
Triangulation with a compass
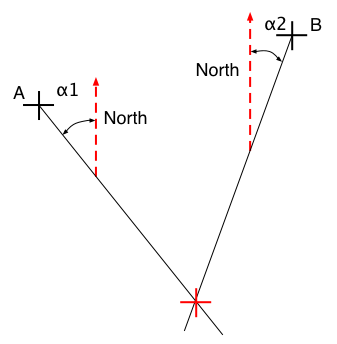
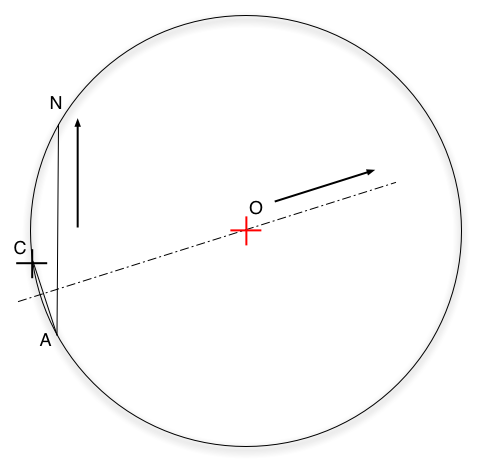
Then you need only 2 landmarks !
You indeed still use 3 landmarks, the last
one only happen to be really, really far away (North direction) and this is
just a special limit case of the previous situation (when the arc of the circle
tend to a segment when N tend towards the North direction)
Slide 18 : 18 / 23 : Intersection between two circles
Intersection between two circles
Given O1(x1,y1,z1), O2(x2,y2,z2), the center of the circles and r1 and r2,
their Radius
Given M(x,y,z) the intersection, then the rought way is ...
| (1) (x - x1)2
+ (y - y1)2 = r12 |
(2) (x - x2)2
+ (y - y2)2 = r22 |
| x2 - 2xx1 + x12
+ y2 -2yy1 + y12 = r12 |
x2 - 2xx2 + x22
+ y2 -2yy2 + y22 = r22 |
| (1) - (2) 2x(x2
- x1) + 2y(y2 - y1) + x12 - x22
+ y12 - y22
= r12 - r22 |
| if x2 - x1 > Epsilon x = (
r12 - r22 -
( 2y(y2 - y1) + x12 - x22
+ y12 - y22)
) / 2(x2 - x1) else y = ... |
Then you replace x within (1) and you solve an equation
of the second degree ...
...piece of cake but ... |
Slide 19 : 19 / 23 : Intersection between two circles (2)
Intersection between two circles (2)
Given O1(x1,y1,z1), O2(x2,y2,z2), the center of the circles and r1 and r2,
their Radius
Given M(x,y,z) the intersection, then another way is ...
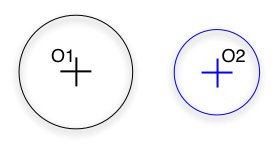
O1O2 > r1 + r2
|
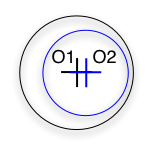
O1O2 < (r1 - r2) and (r1>r2)
NB.: what if r1 = r2 ?
|
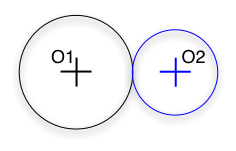
O1O2 = r1 + r2
|
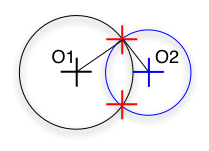
r1 - r2 < O1O2 < r1 + r2
|
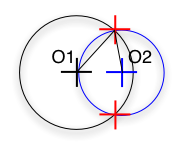
r1 - r2 < O1O2 < r1 + r2
|
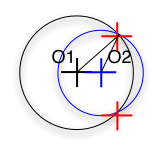
r1 - r2 < O1O2 < r1 + r2
|
NB. : when you see " = 0 " in Maths, you translate
into "< Epsilon" in Computer
Slide 20 : 20 / 23 : Intersection between two circles (3)
Intersection between two circles (3)
Given O1(x1,y1,z1), O2(x2,y2,z2), the center of the circles and r1 and r2,
their Radius
Given M(x,y,z) the intersection, then another way is ...
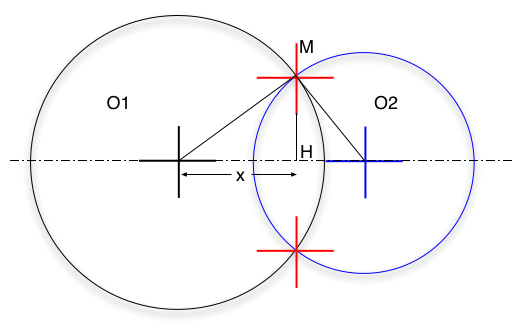 O1H = x
O1H = x
MH = h
0102 = d
H02 = d - x
(1) R12
= h2 + x2
(2) R22
= h2 + (d - x )2
= h2 + d2 -2dx +
x2
(2) - (1) R22
- R12 = d2
- 2dx
=> x = (d2
- R22 + R12)/2d
(1) h = +/- squareroot(R12
- x2)
M = O1 + O1
H +/- HM
Then O1H = x. O1O2/||O1O2||
then inverse -x and y of O1O2/||O1O2|| vector to get an orthogonal vector
Slide 21 : 21 / 23 : Intersection between two circles (4)
Intersection between two circles (4)
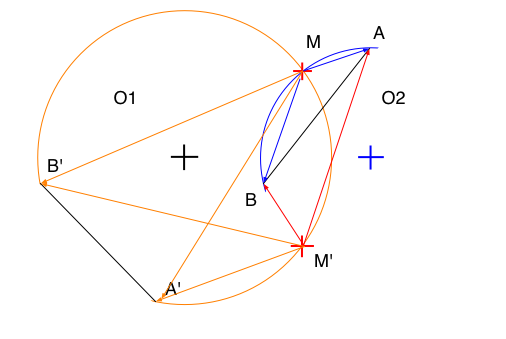
AMB : Obtuse
AM'B, A'M'B', A'MB' : Acute
AMB obtuse <=> MA . MB < 0
What if AMB is a right angle ?
Then we have to be sur of the sign of the
angle
Slide 22 : 22 / 23 : Exercise from Last year Exam
Exercise from Last year Exam
Question 16 ( 8 marks ) :
Write an algorithm (Java-like pseudocode) that will calculate the point of
intersection of a ray (semi segment) and a triangle. The method should return
the status of the intersection (intersect or not, and, if not, why not ). If
it intersects, then the method should also return the coordinates of the intersection.
Use comments in your code to explain the algorithm.
The ray is defined by the origin point O and the direction vector V.
The triangle is defined by the 3 vertices P0, P1, P2.
Tip : if vertices A, B, C and D are on the same plane and if D = A + sAB +
tAC then D is inside triangle ABC if and only if s>=0, t>=0 and s+t <=
1
-
First compute the intersection point M between the ray and the plane of
the triangle
-
Then compute s and t such as M = P0 + s
P0P1 + t P0P2
-
Considering that M is inside the triangle if and only if s
>= 0, t >= 0 and s+t <= 1 draw your conclusion
Slide 23 : 23 / 23 : Exercise from Last year Exam
Exercise from Last year Exam
Question 16 ( 8 marks ) :
Write an algorithm (Java-like pseudocode) that will calculate the point of
intersection of a ray (semi segment) and a triangle. The method should return
the status of the intersection (intersect or not, and, if not, why not ). If
it intersects, then the method should also return the coordinates of the intersection.
Use comments in your code to explain the algorithm.
The ray is defined by the origin point O and the direction vector V.
The triangle is defined by the 3 vertices P0, P1, P2.
Tip : if vertices A, B, C and D are on the same plane and if D = A + sAB +
tAC then D is inside triangle ABC if and only if s>=0, t>=0 and s+t <=
1
-
First compute the intersection point M between the ray and the plane of
the triangle
-
Then compute s and t such as M = P0 + s
P0P1 + t P0P2
-
Considering that M is inside the triangle if and only if s
>= 0, t >= 0 and s+t <= 1 draw your conclusion
Next Week...








 O1H = x
O1H = x 