Parametric curves

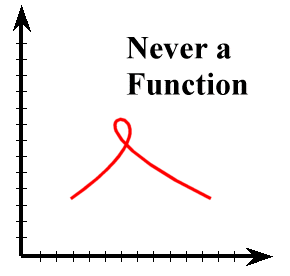Parametric curves are very flexible They are not required to be functions Curves can be multi-valued with respect to any coordinate system (a functions return one unique value for a given entry) Parameter count generally gives the objects's dimension Hyperplane : (n-1 parameter) in space of dimension n , Decouples dimension of object from the dimension of the space r(u) (instead of [x(u), y(u), z(u)]) : vector-valued parametric curve Notion of finite or infinite length : close (could always be bring back to [0 ; 1]) or open interval for u

 

In Cartesian space, a point is defined by distances from the origin along the three mutually orthogonal axes x, y, and z. In vector algebra, a point is often defined by a position vector r, which is the displacement with the initial point at the origin. The path of a moving point is then described by the position vectors at successive values of the parameter, say u Î Â. Hence, the position vector r is a function of u, i.e., r = r(u). In the literature, r(u) is called the vector-valued parametric curve. Representing a parametric curve in the vector-valued form allows a uniform treatment of two-, three-, or n-dimensional space, and provides a simple yet highly expressive notation for n-dimensional problems. Thus, its use allows researchers and programmers to use simple, concise, and elegant equations to formalize their algorithms before expressing them explicitly in the Cartesian space. For these reasons, a vector-valued parametric form is used intensively for describing geometric shapes in computer graphics and computer aided geometric design.

It should be noted that the curve r(u) is said to have an infinite length if the parameter is not restricted in any specific interval, i.e., u Î (-¥,+¥). Conversely, the curve r(u) is said to have a finite length if u is within a closed interval, for example, u Î [a,b] where a, b Î Â. Given a finite parametric interval [a,b], a simple reparametrization t = (u-a)/(b-a) would normalize the parametric interval to t Î [0,1].

A comprehensive study on curves, including polynomial parametric curves, is beyond the scope of this chapter. Interested readers may find such information in many text books on algebraic curves. In this chapter, we discuss only two types of parametric curves, namely Bézier curves and B-spline curves. In particular, we are concerned with the representation of Bézier and B-spline curves as well as some essential geometric processing methods required for displaying and manipulating curves.